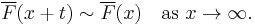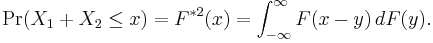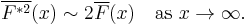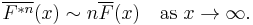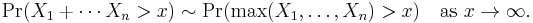Heavy-tailed distribution
In probability theory, heavy-tailed distributions are probability distributions whose tails are not exponentially bounded:[1] that is, they have heavier tails than the exponential distribution. In many applications it is the right tail of the distribution that is of interest, but a distribution may have a heavy left tail, or both tails may be heavy.
There are two important subclasses of heavy-tailed distributions, the long-tailed distributions and the subexponential distributions. In practice, all commonly used heavy-tailed distributions belong to the subexponential class.
There is still some discrepancy over the use of the term heavy-tailed. There are two other definitions in use. Some authors use the term to refer to those distributions which do not have all their power moments finite; and some others to those distributions that do not have a variance. The definition given in this article is the most general in use, and includes all distributions encompassed by the alternative definitions, as well as those distributions such as log-normal that possess all their power moments, yet which are generally acknowledged to be heavy-tailed. (Occasionally, heavy-tailed is used for any distribution that has heavier tails than the normal distribution.)
Contents |
Definition of heavy-tailed distribution
The distribution of a random variable X with distribution function F is said to have a heavy right tail if[1]
This is also written in terms of the tail distribution function
as
This is equivalent to the statement that the moment generating function of F, MF(t), is infinite for all t > 0[2].
The definitions of heavy-tailed for left-tailed or two tailed distributions are similar.
Definition of long-tailed distribution
The distribution of a random variable X with distribution function F is said to have a long right tail[1] if for all t > 0,
or equivalently
This has the intuitive interpretation for a right-tailed long-tailed distributed quantity that if the long-tailed quantity exceeds some high level, the probability approaches 1 that it will exceed any other higher level: if you know the situation is bad, it is probably worse than you think.
All long-tailed distributions are heavy-tailed, but the converse is false, and it is possible to construct heavy-tailed distributions that are not long-tailed.
Subexponential distributions
Subexponentiality is defined in terms of convolutions of probability distributions. For two independent, identically distributed random variables 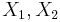 with common distribution function
with common distribution function  the convolution of
the convolution of  with itself,
with itself, 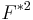 is defined, using Lebesgue-Stieltjes integration, by:
is defined, using Lebesgue-Stieltjes integration, by:
The n-fold convolution 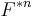 is defined in the same way. The tail distribution function
is defined in the same way. The tail distribution function 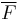 is defined as
is defined as 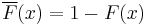 .
.
A distribution  on the positive half-line is subexponential[1] if
on the positive half-line is subexponential[1] if
This implies[3] that, for any 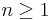 ,
,
The probabilistic interpretation[3] of this is that, for a sum of  independent random variables
independent random variables  with common distribution
with common distribution  ,
,
This is often known as the principle of the single big jump[4].
A distribution  on the whole real line is subexponential if the distribution
on the whole real line is subexponential if the distribution 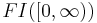 is[5]. Here
is[5]. Here 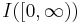 is the indicator function of the positive half-line. Alternatively, a random variable
is the indicator function of the positive half-line. Alternatively, a random variable  supported on the real line is subexponential if and only if
supported on the real line is subexponential if and only if 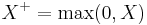 is subexponential.
is subexponential.
All subexponential distributions are long-tailed, but examples can be constructed of long-tailed distributions that are not subexponential.
Common heavy-tailed distributions
All commonly used heavy-tailed distributions are subexponential.[3]
Those that are one-tailed include:
- the Pareto distribution;
- the Log-normal distribution;
- the Lévy distribution;
- the Weibull distribution with shape parameter less than 1;
- the Burr distribution;
- the Log-gamma distribution;
- the Log-Cauchy distribution, sometimes described as having a "super-heavy tail" because it exhibits logarithmic decay producing a heavier tail than the Pareto distribution.[6][7]
Those that are two-tailed include:
- The Cauchy distribution, itself a special case of both the stable distribution and the t-distribution;
- The family of stable distributions,[8] excepting the special case of the normal distribution within that family. Some stable distributions are one-sided (or supported by a half-line), see e.g. Lévy distribution. See also financial models with long-tailed distributions and volatility clustering.
- The t-distribution.
- The skew lognormal cascade distribution.[9]
See also
References
- ^ a b c d Asmussen, Søren (2003). Applied probability and queues. Berlin: Springer. ISBN 9780387002118.
- ^ Rolski, Schmidli, Scmidt, Teugels, Stochastic Processes for Insurance and Finance, 1999
- ^ a b c Embrechts, Paul; Claudia Klüppelberg; Mikosch, Thomas (1997). Modelling Extremal Events for Insurance and Finance. Berlin: Springer. ISBN 9783540609315.
- ^ Foss, Konstantopolous, Zachary, "Discrete and continuous time modulated random walks with heavy-tailed increments", Journal of Theoretical Probability, 20 (2007), No.3, 581—612
- ^ Willekens, E. Subexponentiality on the real line. Technical Report, K.U. Leuven(1986)
- ^ Falk, M., Hüsler, J. & Reiss, R. (2010). "Laws of Small Numbers: Extremes and Rare Events". Springer. p. 80. ISBN 9783034800082.
- ^ Alves, M.I.F., de Haan, L. & Neves, C. (March 10, 2006). "Statistical inference for heavy and super-heavy tailed distributions". http://docentes.deio.fc.ul.pt/fragaalves/SuperHeavy.pdf.
- ^ John P. Nolan (2009). "Stable Distributions: Models for Heavy Tailed Data" (PDF). http://academic2.american.edu/~jpnolan/stable/chap1.pdf. Retrieved 2009-02-21.
- ^ Stephen Lihn (2009). "Skew Lognormal Cascade Distribution". http://www.skew-lognormal-cascade-distribution.org/.
![\lim_{x \to \infty} e^{\lambda x}\Pr[X>x] = \infty \quad \mbox{for all } \lambda>0.\,](/2012-wikipedia_en_all_nopic_01_2012/I/51749065412557a426e5851f14ca8a78.png)
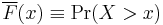
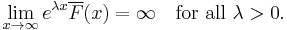
![\lim_{x \to \infty} \Pr[X>x%2Bt|X>x] =1, \,](/2012-wikipedia_en_all_nopic_01_2012/I/639998d90c0c71e83c67a153ab2d6b2e.png)